Cours/TD n°3bis : les boucles
Découpons le problème
Nous avons plusieurs utilisations des boucles… C’est précisément ce qui rend difficile leur création. Vu la difficulté, nous allons séparer les différentes utilisations des boucles. Voyons donc quelle est la première utilisation des boucles :
Une boucle pour attendre un évènement…
Prenons l’exemple de CounterStrike. Lorsque vous lancez une partie, après un court chargement, le décor, les adversaires et les informations sur le joueur s’affichent. Cet affichage est extrêmement complexe (et sort de ce que je dois vous apprendre), mais il est facile de comprendre comment est structuré le programme. Le programme utilise une boucle qui affiche le décor, et qui ne s’arrête que lorsque l’utilisateur se déconnecte. Pour simplifier, on va supposer qu’en appuyant sur “Esc”, l’utilisateur se déconnecte… Ainsi, le programme de CounterStrike est quelque chose comme :
Var touche : chaine
Debut
toucheAppui <- “”
TantQue non(toucheAppui=“Esc”) faire
Afficher une image
Saisir touche
FinTantQue
Fin
La première utilisation d’une boucle (et la plus souvent utilisée) est d’attendre qu’un événement devienne faux. Dans cet exemple, la boucle permet d’attendre que l’utilisateur appuie sur “Esc” pour quitter. En effet, tant que la touche pressée n’est pas égale à “Esc”, on exécute les instructions à l’intérieur de la boucle (et donc on affiche les images du décor…).
Important :
Il y a donc deux choses à préciser quand on fait une boucle de ce type : qu’est ce qu’on attend, et qu’est ce qu’on fait pendant qu’on attend ?
- En répondant à « qu’est ce qu’on attend ? », on définit la condition de la boucle. Cette condition doit être vraie lorsqu’on attend, et fausse quand on a fini d’attendre. Si c’est l’inverse, on peut utiliser le mot clef « non » qui permet d’inverser la condition.
- En répondant à « qu’est ce qu’on fait pendant qu’on attend ? », on définit le contenu de la boucle. Le contenu consiste en général à afficher quelque chose, puis redemander une valeur à l’utilisateur. Il est possible de mettre des Si-Alors-Sinon, ce qui permet d’afficher un message différent suivant la valeur saisie par l’utilisateur.
Mise en pratique :
Souligner dans les énoncés ce qui doit permettre de répondre aux deux questions « qu’est ce qu’on attend ? » et « qu’est ce qu’on fait pendant qu’on attend ? » pour les exercices suivants :
- Ecrire un algorithme qui demande à l’utilisateur s’il veut du café. Tant que l’utilisateur n’a pas saisi ‘O’ ou ‘N’, redemander à l’utilisateur de saisir un nouveau nombre.
- Ecrire un algorithme qui demande à l’utilisateur un nombre jusqu’à ce que ce nombre soit compris entre 1 et 3.
- Ecrire un algorithme qui reproduit le fonctionnement d’une caisse enregistreuse. Tant que le prix est différent de zéro, l’ordinateur va demander à l’utilisateur de saisir le montant des articles, puis qui affiche la somme du montant de tous les articles.
- Ecrire un algorithme qui demande un nombre compris entre 10 et 20, jusqu’à ce que la réponse convienne. En cas de réponse supérieure à 20, on fera apparaître un message : « Plus petit ! », et inversement, « Plus grand ! » si le nombre est inférieur à 10.
Reprendre les exercices et répondre à la question « qu’est ce qu’on attend ? » sous forme algorithmique (c'est-à-dire avec des noms de variables et des opérateurs de comparaisons : >, <, =, ≠…) pour que l’expression soit fausse quand on doit quitter la boucle.
Reprendre les exercices et répondre à la question « qu’est ce qu’on fait pendant qu’on attend ? » sous forme algorithmique, sans se soucier des déclarations de variables.
Une boucle pour compter
La deuxième utilisation des boucles ne devrait pas poser de problèmes si vous avez compris l’utilisation des premières boucles. En effet, c’est exactement le même principe qu’avant, c'est-à-dire que l’on va attendre qu’une condition se réalise. Seulement, dans ce cas, on va utiliser une variable en plus pour compter le nombre de tours que l’on fait. La variable s’appelle en général un compteur…
Important :
La boucle est donc définie de la même manière qu’avant (c'est-à-dire en répondant aux deux questions), et on rajoute dans la boucle une variable qui compte le nombre de fois qu’on a exécuté la boucle. Il est alors possible de faire beaucoup de choses : on peut afficher la valeur du compteur après la boucle, ce qui permet de savoir combien de fois on a utilisé la boucle, mais on peut aussi afficher la valeur du compteur dans la boucle, ce qui permet d’afficher des choses comme « c’est votre 3eme essais... ». L’utilisation la plus courante permet de donner un nombre d’exécutions maximal. En effet, puisque la variable compte le nombre d’exécutions de la boucle, il est possible de s’en servir pour dire, par exemple, que l’on veut qu’il n’y ait pas plus de 10 exécutions de la boucle. Dans la condition de la boucle (qui, je le rappel, est la réponse à la question « qu’est ce qu’on attend ? »), on va alors rajouter à la fin de la condition “ET compteur < 10“.
Mise en pratique :
Ecrire les algorithmes suivants :
- Ecrire un algorithme qui demande un nombre compris entre 10 et 20, jusqu’à ce que la réponse convienne. En cas de réponse supérieure à 20, on fera apparaître un message : « Plus petit ! », et inversement, « Plus grand ! » si le nombre est inférieur à 10. Une fois que l’utilisateur a saisi un bon nombre, le programme affiche le nombre d’essais que l’utilisateur a eu.
- Reprendre l’algorithme précédent, et quitter la boucle si l’utilisateur s’est trompé plus de 3 fois.
- Ecrire un algorithme qui calcule le prix total d’un caddie. Pour cela, l’utilisateur saisie le prix des articles du caddie, jusqu’à ce qu’il entre un nombre négatif ou nul. Le programme affiche ensuite la somme à l’écran.
- Reprendre l’algorithme précédent pour qu’il affiche en plus le nombre d’articles que l’utilisateur a saisi.
- Ecrire un algorithme qui demande à l’utilisateur de saisir un mot de passe à l’utilisateur, et tant que l’utilisateur ne saisi pas « xyz », redemande à l’utilisateur de saisir le mot de passe.
- Reprendre l’algorithme précédent pour qu’il ne soit pas possible de saisir plus de 3 fois le mot de passe.
Une boucle pour calculer.
La dernière utilisation des boucles (et la plus complexe) consiste à utiliser les boucles pour faire un calcul. Le cas le plus simple (relativement) consiste à faire le même calcul plusieurs fois. Dans le cas le plus compliqué, il faut faire un calcul différent suivant le nombre de boucles que l’on a fait. Dans tous les cas, il est nécessaire d’utiliser une variable supplémentaire pour stocker le résultat du calcul. Cette variable permet alors d’utiliser le résultat du calcul de la précédente boucle. Prenons par exemple l’algorithme suivant :
Ecrire un algorithme qui demande un nombre de départ, et qui calcule sa factorielle.
NB : la factorielle de 8, notée 8 !, vaut 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
La première chose à faire, c’est de savoir quand on veut s’arrêter. On voit ici que le calcul est terminé quand on aura fait 7 multiplications. Avec l’habitude, et à force de persévérance, on pourra se dire qu’on a besoin d’une boucle avec un compteur. Pourquoi ? Parce qu’on voit qu’il y a un nombre d’opérations qui peut être déduit du chiffre que l’utilisateur saisi. Maintenant essayons de savoir comment utiliser le compteur et la boucle. Pour ça, on décompose le calcul :
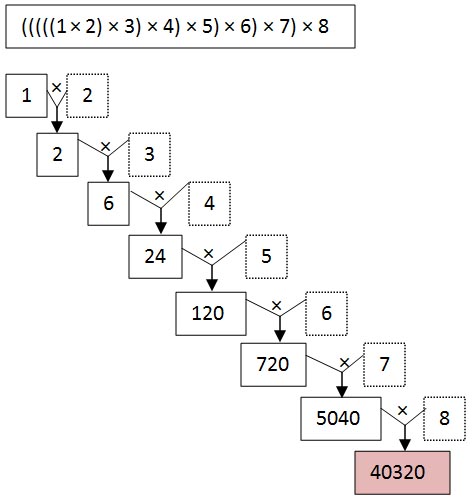
Grace à cette décomposition, on voit apparaitre une chose qu’il faut absolument reconnaitre : la valeur des carrés en pointillés se suit ! Voir cette organisation doit absolument déclencher chez vous une irrésistible envie d’utiliser un compteur ! En effet, une série de nombres qui se suivent correspond souvent à la valeur d’un compteur dans une boucle.
On a aussi la condition d’arrêt : il faut faire 7 opérations, soit une fois de moins que le nombre saisi par l’utilisateur… En général, il faut trouver un lien entre le nombre d’opérations et le nombre que l’utilisateur a saisi. Dans notre cas, on quitte la boucle quand on aura fait 7 opérations, donc quand on aura fait (nombre -1) opérations !
Enfin, on se rend compte qu’à chaque opération, le résultat est égal au résultat précédent multiplié par le compteur. Ça y est, on a le contenu de la boucle : resultat <- resultat * compteur.
Mise en pratique :
Quel est le (ou les) bon programmes :
|
compteur <- 1
resultat <- 2 tantque compteur < nombre faire resultat <- resultat*compteur compteur <- compteur+1 finTantQue Afficher nombre,“ != ”,resultat |
compteur <- 2
resultat <- 2 tantque compteur < nombre faire resultat <- resultat*compteur compteur <- compteur+1 finTantQue Afficher nombre,“ != ”,resultat |
|
compteur <- 1
resultat <- 1 tantque compteur < nombre faire resultat <- resultat*compteur compteur <- compteur+1 finTantQue Afficher nombre,“ != ”,resultat |
compteur <- 2
resultat <- 1 tantque compteur < nombre faire resultat <- resultat*compteur compteur <- compteur+1 finTantQue Afficher nombre,“ != ”,resultat |
Sur le même principe, écrire les algorithmes suivants :
-
Ecrire un algorithme qui demande un nombre de départ (un entier), et qui calcule la somme des entiers jusqu’à ce nombre. Par exemple, si l’on entre 5, le programme doit afficher 15 :
1 + 2 + 3 + 4 + 5 = 15 -
Reprendre l’algorithme précédent pour qu’il ne fasse la somme que des nombre pairs. Par exemple, si l’on entre 7, le programme doit afficher 12 :
2 + 4 + 6 = 12 -
Ecrire un algorithme qui demande deux entiers à l’utilisateur et qui calcule la somme des entiers compris entre ces deux valeurs. Par exemple, si l’on entre 7 et 12, le programme doit afficher 57 :
7 + 8 + 9 + 10 + 11 + 12 = 57
Une dernière utilisation des boucles…
Il arrive qu’au moment d’écrire le programme, le nombre de tours de boucle nécessaires soit connu. C’est le cas, par exemple lorsque l’on cherche à calculer la moyenne de 10 notes. On sait que le même calcul sera fait 10 fois. Dans ce cas, il existe une structure qui permet de simplifier la vie du programmeur. Cette boucle s’appelle la boucle Pour.
Insistons : la structure « Pour … FinPour » n’est pas du tout indispensable ; on pourrait fort bien programmer toutes les situations de boucle uniquement avec un « Tant Que ». Le seul intérêt du « Pour » est d’épargner un peu de fatigue au programmeur, en lui évitant de gérer lui-même la progression de la variable qui lui sert de compteur (on parle d’incrémentation, encore un mot qui fera forte impression sur votre entourage).
La syntaxe de la boucle est la suivante :
Instructions
FinPour
Il est donc possible de définir l’intervalle de valeurs dans laquelle la variable va évoluer. C’est le rôle de init et de final.
Il est aussi possible de définir une progression un peu spéciale, de 2 en 2, ou de 3 en 3. Ce n’est pas un problème : il suffira de le préciser à votre instruction « Pour » en lui rajoutant le mot « Pas de » et la valeur de ce pas (Le « pas » dont nous parlons, c’est le « pas » du marcheur, « step » en anglais).
Remarque.
Dans une structure Pour, il ne faut surtout pas essayer de modifier la valeur du compteur. En effet, la boucle pour change automatiquement sa valeur à chaque passage, et la modifier manuellement entraine un plantage quasi inévitable.
Mise en pratique :
Reprendre les exercices, et détectez ceux qui peuvent être utilisés avec une boucle Pour. Dans ce cas, réécrivez l’algorithme.




