Cours/TD n°2 : les conditions
Qu’est ce qu’une condition ?
Pour l’instant, nous avons vu comment demander à l’ordinateur de calculer le résultat d’un calcul. La structure d’un algorithme est donc bien souvent la même et se résume à demander à l’utilisateur de saisir une (ou plusieurs) variable, puis de faire des calculs avec cette (ou ces) variable, pour enfin l’afficher à l’écran. Cependant, cette méthode de programmation ne permet pas de prévoir différentes manières d’agir, en fonction des valeurs entrées par l’utilisateur.
Pour prendre un exemple, imaginons qu’on écrive un programme qui affiche une recette. Normalement, l’algorithme ressemblera à quelque chose comme : « mettez de l’huile d’olive dans la poêle, versez les oignons et le miel, faites cuire à feux doux pendant 10 minutes et servez ». Mais pour rendre la recette plus générale, vous pouvez avoir envie de rajouter des alternatives : « mettez de l’huile d’olive dans la poêle (si vous n’en avez pas, mettez de la margarine), versez les oignons et le miel, faites cuire à feux doux pendant 10 minutes (si les ognons ne sont pas caramélisés, faites cuire 5 minutes de plus) et servez ».
Le deuxième algorithme a ceci de supérieur au premier qu’il prévoit, en fonction d’une situation pouvant se présenter de deux façons différentes, deux façons différentes d’agir. Cela suppose que l’interlocuteur (le cuisinier) sache analyser la condition que nous avons fixée à son comportement (« Ai-je de l’huile d’olive ? Est-ce que mes oignons sont caramélisés ?») pour effectuer la série d’actions correspondante.
Quelles structures ?
Il n’y a que deux formes possible pour réaliser ces alternatives. La première est la plus simple, tandis que la seconde est plus complexe :
|
Si booléen Alors Instructions Finsi |
|
Si booléen Alors Instructions 1 Sinon Instructions 2 Finsi |
Quelques explications. Tout d’abord, on remarque qu’il faut un booléen après le Si. Ce booléen peut être uniquement VRAI ou FAUX, et n’a que deux origines : une variable ou une expression.
L’utilisation de ces instructions est alors très claire : dans la forme la plus simple, l’ordinateur teste la valeur du booléen (ou de l’expression), et si la valeur est évaluée à VRAI, alors l’ordinateur exécute les instructions, jusqu'à rencontrer le mot Finsi. Il peut y avoir une instruction ou cent, ça n’a pas d’importance. Ce qu’il faut savoir, c’est que dans le cas où le booléen est évalué à faux, alors l’ordinateur va passer directement aux instructions qui suivent le Finsi.
Dans le cas complet, c’est à peine plus compliqué. Si le booléen est évalué à vrai, alors on exécute les instructions entre le alors et le sinon, puis on passe aux instructions qui suivent le Finsi. Sinon, les instructions entre le sinon et le finsi sont exécutées, puis celles qui suivent le Finsi.
En fait, la structure simple correspond au cas où l’une des deux branches du Si est vide (c'est-à-dire qu’il n’y a pas de alors ou de sinon). Par exemple, dire « si l’utilisateur a entré un bon mot de passe, on affiche bravo » ne nécessite pas de sinon. Par contre, dire « si l’utilisateur a entré un bon mot de passe, on affiche “bravo”, autrement afficher “erreur” » nécessite l’utilisation d’un alors et d’un sinon.
Mise en pratique :
Identifier le nombre de variables et le type de structure (si-alors-finsi ou si-alors-sinon-finsi) à utiliser pour concevoir ces algorithmes :
1. Ecrire un algorithme qui demande à l’utilisateur de saisir un nombre et qui affiche le signe du nombre (« + » ou « - »)
2. Ecrire un algorithme qui affiche « OK » si la valeur entrée par l’utilisateur est comprise entre 30 et 40.
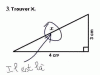
3. Écrire en pseudo-code un programme qui demande à l’utilisateur de saisir les valeurs des trois côtés d’un triangle et affiche « Rectangle ! » si le triangle est rectangle.
4. Ecrire un algorithme qui demande à l’utilisateur quel est son âge et qui affiche si l’utilisateur est majeur ou non.
5. Écrire l’algorithme qui demande à l’utilisateur de saisir les valeurs des trois côtés d’un triangle et qui affiche « premier » si la première valeur est la plus petite, « second » si la seconde valeur est la plus petite et enfin « dernier » si c’est la troisième valeur la plus petite.
Les conditions
Nous avons vu que l’ordinateur se base sur la valeur du booléen qui suit le Si pour évaluer quelles instructions exécuter. Ce qui nous manque maintenant, c’est de savoir quoi mettre après le Si pour que l’expression booléenne soit valide. Nous avons dit précédemment que le booléen n’a que deux origines : une variable ou une expression. Dans le cas d’une variable, c’est très simple : il suffit de mettre le nom de la variable et, à l’exécution, l’ordinateur regardera le contenu de la variable (ce qu’il y a dans la boite) et déterminera quelle branche exécuter. Cependant, le plus souvent, nous utiliserons plutôt une expression conditionnelle. Sous ce nom barbare se cache en réalité un concept bien simple : la comparaison. Ce concept est très important, puisqu’il conditionne la manière d’écrire l’expression : elle sera TOUJOURS construite ainsi :
- Une valeur
- Un opérateur de comparaison
- Une autre valeur
Les valeurs peuvent être de n’importe quel type (entier, caractère, chaine…) mais pour que l’expression ait un sens, il faut que les deux valeurs aient un type compatible. Par exemple, il est difficile de comparer une chaine avec un entier… Par contre, comparer un entier avec un réel est valide.
Les opérateurs de comparaison sont au nombre de six : < , > , = , ≤ , ≥, ≠. A noter qu’ils sont utilisables avec les caractères ou les chaines (dans ce cas, c’est l’ordre alphabétique qui est utilisé).
Mise en pratique :
Reprendre les exercices de la première feuille et écrire les algorithmes 1, 3 et 4 :
|
Programme Exo Var .................................. : .............. .................................. : .............. .................................. : .............. .................................. : .............. Debut Fin |
Conditions composées
En formulant une condition dans un algorithme, il faut se méfier comme de la peste de certains raccourcis du langage courant, ou de certaines notations valides en mathématiques, mais qui mènent à des non-sens informatiques. Prenons par exemple la phrase « Toto est compris entre 5 et 8 ». On peut être tenté de la traduire par : 5 < Toto < 8.
Or, une telle expression, qui a du sens en français, comme en mathématiques, ne veut rien dire en programmation. En effet, elle comprend deux opérateurs de comparaison, soit un de trop, et trois valeurs, soit là aussi une de trop. Il est donc nécessaire de « casser » en deux cette condition. En effet, dans la condition « Toto est compris entre 5 et 8 », il se cache deux conditions valide en algorithme : « Toto est supérieur à 5 » ET « Toto est inferieur à 8 ».
Il est donc possible de lier deux conditions par un mot clé appelé « opérateur logique ». Ces opérateurs se comportent alors exactement comme des portes logiques. C'est-à-dire que les entrées de l’opérateur logique sont les deux expressions booléennes, et la sortie sera la valeur testée par l’ordinateur pour décider quelle branche exécuter.
Mise en pratique :
Remplir les tables de vérités suivantes :
|
OU |
Vrai |
Faux |
|
Vrai |
|
|
|
Faux |
|
|
|
ET |
Vrai |
Faux |
|
Vrai |
|
|
|
Faux |
|
|
Evaluer les conditions suivantes (Vrai ou Fausse), avec : Titi=2, Toto= 4, Tutu=’c’, Tata=“Salut ”
1. Titi=2 ET “Toto”=“4”
2. Titi≠Toto ET (Toto=2 OU Tata<“Toto”)
3. Titi≠Toto ET (Toto=2 OU Tata<“Toto”)
4. Titi<4 ET Toto>2 ET Tutu>’a’ ET Tata<“Zoro” ET 4<3
5. Titi<4 OU Toto>2 OU Tutu>’a’ OU Tata<“Zoro” OU 4<3
6. Toto>Titi ET Tutu=’c’ ET Tata=“Tutu”
7. Pouet>4 ET Pouet<2
Créer les conditions correspondant aux situations suivantes (en majuscule, les variables…):
1. Faite une condition évaluée à vrai quand le guichet est ouvert : Un guichet est ouvert tous les jours après 12h, sauf le samedi où il est fermé toute la journée (JOUR est un entier, avec Lundi=1 et Dimanche=7, et HEURE est un entier).
2. Faite une condition évaluée à vrai quand l’eau est liquide : L’eau gèle quand TEMP est inférieur à 0°C et devient de la vapeur quand TEMP est supérieur à 100°C. Dans tout les autres cas, elle est liquide.
3. Faite une condition évaluée à vrai quand l’ordinateur plante : Un ordinateur plante quand TEMP_PROC est supérieur à 80°C ou que SYSTEM est « windows » et que VERSION est égal à « vista ».
4. Faite une condition évaluée à faux quand l’étudiant travaille : Un étudiant ne travaille jamais sauf quand sa MOYENNE est inferieur à 10 ou qu’il a eu plus de 3 AVERTISSEMENT.
Tests imbriqués
Graphiquement, on peut très facilement représenter un SI comme un aiguillage de chemin de fer. Un SI ouvre donc deux voies, correspondant à deux traitements différents. Mais il y a des tas de situations où deux voies ne suffisent pas. Par exemple, un programme devant donner l’état de l’eau selon sa température doit pouvoir choisir entre trois réponses possibles (solide, liquide ou gazeuse).
Il y a deux manières de résoudre ce problème :
Début
Ecrire "Température de l’eau ?"
Lire Temp
Si Temp =< 0 Alors
Ecrire "C’est de la glace"
Sinon
Si Temp < 100 Alors
Ecrire "C’est du liquide"
Sinon
Ecrire "C’est de la vapeur"
Finsi
Finsi
Fin
Début
Ecrire "Température de l’eau ?"
Lire Temp
Si Temp =< 0 Alors
Ecrire "C’est de la glace"
FinSi
Si Temp > 0 Et Temp < 100 Alors
Ecrire "C’est du liquide"
Finsi
Si Temp > 100 Alors
Ecrire "C’est de la vapeur"
Finsi
Fin
La deuxième solution est meilleure pour plusieurs raisons :
- Les conditions sont plus simples (pas de ET)
- L’ordinateur n’a pas à tester toutes les conditions si par exemple la température est < à 0 (la première condition étant vrai, l’ordinateur affiche « C’est de la glace » et passe tout de suite au FinSi).
- Le code est plus lisible (pas de conditions à rallonges…)
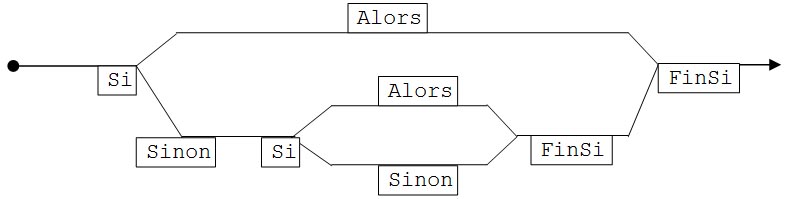
Une structure SI peut être facilement comparée à un aiguillage de train. La voie principale se sépare en deux, le train devant rouler ou sur l’une, ou sur l’autre, et les deux voies se rejoignant tôt ou tard pour ne plus en former qu’une seule, lors du FinSi. On peut schématiser cela ainsi :

Dans le cas d’une imbrication de Si (comme c’est le cas pour l’eau dans le deuxième exemple), les aiguillages deviennent un peu plus compliqués, ce qui donne :
Mise en pratique :
Ecrire les algorithmes suivant :
1. Ecrire un algorithme qui demande trois noms à l’utilisateur et l’informe ensuite s’ils sont rangés ou non dans l’ordre alphabétique.
2. Ecrire un algorithme qui demande un nombre à l’utilisateur, et si le nombre est différent de zéro, demande un autre nombre et si cet autre nombre est positif il affiche le résultat de leur division. Dans tout les autres cas, le programme affiche « Erreur de saisie… ».
3. Un magasin de reprographie facture 0,10 € les dix premières photocopies, 0.09 € les vingt suivantes et 0.08 € au-delà. Ecrivez un algorithme qui demande à l’utilisateur le nombre de photocopies effectuées et qui affiche la facture correspondante sous cette forme (si l’utilisateur à demandé 3 impressions) :
Facture d’impression :
3 impressions : 0.3 €
*****************
4. Ecrire un algorithme qui demande l’âge d’un enfant à l’utilisateur. Ensuite, il l’informe de sa catégorie :
- "Poussin" de 6 à 7 ans
- "Pupille" de 8 à 9 ans
- "Minime" de 10 à 11 ans
- "Cadet" après 12 ans
5. Faire les algorithmes de la première feuille.